BECE 1995 - MATHEMATICS [PAPER II]
THEORY QUESTIONS
(a)
There are 20 students in a hostel. 16 of them are fluent in French and 10 of them are fluent in English. Each student is fluent in at least one of the two languages.
(i)
Illustrate this information on a Venn diagram
(ii)
How many students are fluent in both English and French?
(b)
The sum of the ages of two brothers Kofi and Kweku is 35. Kofi's age is two-thirds of Kweku's age. Find their ages.
(a)
Using a ruler and a pair of compasses only
(i)
construct triangle ABC such that |AB| = 9 cm, angle BAC = 60° and angle ABC = 45°.
(ii)
construct a line from the point C perpendicular to line AB and let it meet AB at P. Measure |CP| and |AP|
(b)
What is the value of angle ACP?
(a)
Mansah earns a salary of ₵10,000.00 per month as a sales girl. In addition to the salary, she is given a commission of 1.5% of whatever sales she makes in a month. In January this year, she made sales of ₵7,500,000.00. What was the total amount Mansah earned at the end of January?
(b)
The diagram below shows a circle with centre O and radius 14 cm. The shaded region AOB is a sector with angle AOB = 72°.
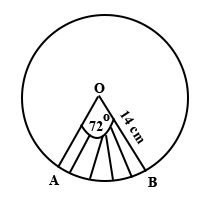
Find:
(i)
The length of the minor arc AB
(ii)
The area of the shaded sector AOB
[Take π =
(a)
Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes, OX and OY on a graph sheet.
(b)
On the graph sheet, mark the x-axis from –5 to 5 and the y-axis from –6 to 6
(c)
(i)
Plot on the same graph sheet the points A(1, 1
(ii)
Join the points to form a triangle. What type of triangle have you drawn?
(d)
Draw the image triangle A1B1C1 of ABC under a reflection in the y-axis, where A→A1, B→B1 and C→C1. Label the vertices and the co-ordinates clearly.
(e)
Draw the image triangle A2B2C2 of triangle ABC under an enlargement with scale factor –1 with the centre of enlargement as the origin (0,0), where A→A2, B→B2 and C→C2. Show all lines of enlargement. Label the vertices and co-ordinates clearly
(f)
What single transformation maps A1B1C1 onto A2B2C2 where A1→A2, B1→ B2 and C1→C2?
(a)
The data below shows the distribution of the ages of workers in a factory.
| Ages (in years) | No. of workers |
| 19 | 3 |
| 24 | 7 |
| 29 | 8 |
| 34 | 4 |
| 39 | 5 |
| 44 | 3 |
(i)
How many workers are there in the factory?
(ii)
What is the modal age of the distribution?
(iii)
Calculate the mean age of the workers, correct to one decimal place.
(b)
(i)
Make T the subject of the relation
I =
(ii)
If I = ₵40,000.00, P = ₵64,000.00 and R = 25%, find the value of T in years.


 TeacherDora Admin
TeacherDora Admin
.jpg)