TeacherDora Admin
BECE 2000- MATHEMATICS [PAPER II]
THEORY QUESTIONS
(a)
Simplify:
(b)
Solve the equation
(c)
If 3y = 2x2 - 3x + 7, find y, when x = 5
(a)
In the diagram, PADQ and RBCS are parallel lines. │BD│ = │DC│, angle ADB = 65° and angle ABR = 50°.
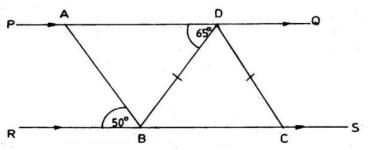
(i)
Calculate the angle BDC.
(ii)
Calculate angle ABD.
(iii)
Find angle BAD.
(iv)
What type of triangle is triangle ABD?
(b)
Using a ruler and a pair of compasses only, construct triangle XYZ, with |YZ| = 8 cm, angle XYZ = 60° and |XY|=9 cm.
Measure
(i)
angle YZX;
(ii)
|XZ|
Ama was granted a loan of ₵800,000.00 by a bank. The rate of interest was 42% per annum.
(a)
Calculate
(i)
the interest at the end of the year;
(ii)
the total amount Ama had to pay at the end of the year.
(b)
Ama was able to pay only ₵700,000.00 at the end of the year.
(i)
Find how much Ama still owed the bank.
(ii)
Express the amount Ama owed after paying the ₵700,000.00 to the bank as a percentage of the loan she took from the bank.
The following is a record of scores obtained by 30 JSS form 2 pupils in a test marked out of 5.
| 5, | 3, | 2, | 4, | 5, | 2, | 4, | 3, | 1, | 1 |
| 3, | 4, | 2, | 3, | 4, | 5, | 3, | 4, | 3, | 2 |
| 4, | 3, | 1, | 2, | 2, | 3, | 3, | 2, | 4, | 3 |
| Score (x) | Tally | Frequency (f) | fx |
(a)
Copy and complete the table.
(b)
Find the mean of the distribution.
(c)
If a pupil is selected at random from the form, what is the probability that he/she scored 4 marks?
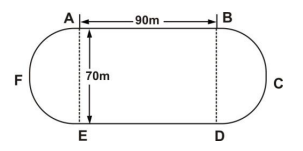
The diagram shows a running track ABCDEFA. AB and ED are the straight sides. The ends AFE and BCD are semi circular shapes.
|AB| = |ED| = 90 m and |AE| = |BD| = 70 m.
Find
(a)
the total length of the two semi circular ends, AFE and BCD;
(b)
the perimeter of the running track ABCDEFA;
(c)
the total area of the running track ABCDEF.
[Take π =