BECE 2003 - MATHEMATICS [PAPER I]
OBJECTIVE TEST
1.
P = {3, 6, 9, 12, 15}. Which of the following best describes the set P?
The set of multiples of 3 less than 18
The set of multiples of 3
The set of odd numbers
The set of odd numbers less than 16
2.
If Q = {2, 4, 6, 7, 8, 10} and R = {3, 5, 7, 9, 10, 11}, find Q ∩ R.
{2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
{7, 10}
{10}
{7}
3.

Find the set of missing numbers on the number line above.
{-21, -6, 11}
{-21, -10, 11}
{-25, -6, 15}
{-25, -10, 15}
4.
If 7.2 and 7.9 are two points on a number line, find the number in the middle of these points.
7.35
7.45
7.55
7.65
5.
Find the least common multiple (LCM) of 12 and 20.
24
48
60
80
6.
Express 72 as a product of prime factors.
2×3
22×32
22×33
23×32
7.
If 3t – 2 (t + 12) = 11, find the value of t.
–35
–13
13
35
8.
What is the value of the digit 8 in the number 78000?
8 ten thousands
8 thousands
8 hundreds
8 tens
9.
Find the product of 17 and 121.
968
1,751
2,057
8,591
10.
Araba owes ₵550,000.00 at the bank. She goes to pay ₵150,000.00. How much does Araba owe the bank now?
₵700,000.00
₵600,000.00
₵500,000.00
₵400,000.00
11.
Evaluate
0.259
2.590
25.900
259.000
12.
Express 1.25 as a mixed fraction in its lowest form.
1
1
1
13.
The total number of match sticks in 6 match boxes was 270. Find the total number of sticks in 20 similar boxes.
710
800
810
900
14.
A car travels at an average speed of 45 km per hour. What distance does it cover in 12 hours?
450 km
480
500 km
540 km
15.
Calculate the simple interest on ₵130,000.00 for 2
₵78,000.00
₵39,000.00
₵36,000.00
₵31,200.00
16.
Express
20%
25%
40%
80%
17.
Kwame gets a commission of 20% on bread sold. In one week, Kwame's commission was ₵45,000.00. How much bread did he sell during that week?
₵205,000.00
₵220,000.00
₵225,000.00
₵235,000.00
18.
Write 83000 in standard form.
8.3x10-4
8.3x10-3
8.3x103
8.3x104
19.
The following marks are the marks obtained by pupils in a test: 2, 3, 5, 2, 3, 4, 2, 3, 5, 3.
Use the information above to answer the question below.
What is the mode?
2
3
4
5
20.
The following marks are the marks obtained by pupils in a test: 2, 3, 5, 2, 3, 4, 2, 3, 5, 3.
Use the information above to answer the question below.
Calculate the mean
3.0
3.2
4.0
4.2
21.
There are 12 red and 8 blue balls in a bag. If a ball is selected at random from the bag, what is the probability that it is red?
22.
If y =
x = 3y - 2
3y + 2
x =
x = -
23.
Simplify 6a2 × 4a2b2
10a4b2
24a2b2
24a4b2
24a2b4
24.
Change 17ten to a base two numeral.
101
1001
1000
10001
25.
Which of the following statements is true?
8+4 < 10
7+4 < 10
6+4 < 10
5+4 < 10
26.
Find the set of integers within the interval -2 < x < 2
{-2,-1,2}
{-2,-1,0}
{-1,0,1}
{-1,1,2}
27.
Use the mapping below to answer the question below.
| x | 1 | 2 | 3 | 4 | 5 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | -4 | -2 | 0 | 2 | m |
What is the rule for this mapping?
x→ 2(x - 3)
x→ x - 5
x→ 2(x - 2)
x→ 2x-3
28.
Use the mapping below to answer the question below.
| x | 1 | 2 | 3 | 4 | 5 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | -4 | -2 | 0 | 2 | m |
Find m.
–4
4
6
8
29.
Which of the following represents the net of a pyramid?
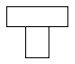
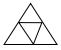
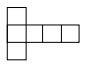
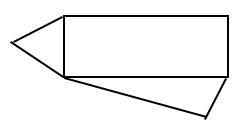
30.
A rectangular tank has dimensions 2.5 m by 4 m by 5 m. It is filled with water to the brim. If 35 m3 of the water is used, how much water is left in the tank?
50 m3
35 m3
25 m3
15 m3
31.
In the triangle XYZ, angle XZY = 90°, |XY| = 13 cm and |YZ| = 5cm.
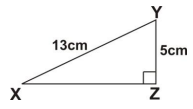
What is the length of XZ?
4 cm
8 cm
12 cm
65 cm
32.
How many lines of symmetry has an equilateral triangle?
1
2
3
4
33.
The value of an obtuse angle lies between
0° and 90°
90° and 180°
90° and 270°
180° and 360°
34.
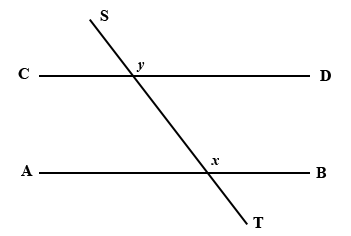
In the diagram above, AB is parallel to CD. Angles x and y are
alternate angles
corresponding angles
vertically opposite angles
co-interior angles
35.
If a =
36.
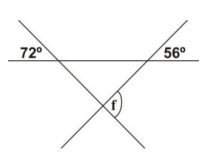
Find the size of the angle marked f, in the diagram above
56°
72°
108°
128°
37.
The dimensions of a cuboid are 2 cm, P cm and 5 cm. Which of the following is an expression for the volume of the cuboid?
7P cm3
(7 + P) cm3
10P cm3
(10 + P) cm3
38.
Simplify 5(3t + 1) – 6(t – 1).
9t + 11
9t + 7
9t + 1
9t – 5
39.
Simplify: (
1
6
40.
The point P moves in a plane such that it is always at equal distance from two fixed points, A and B in the same plane. Which of these is the locus of the point P?
The bisector of angle PAB
A circle centre B and radius AB
A circle with AB as the diameter
The perpendicular bisector of line AB.


 TeacherDora Admin
TeacherDora Admin