TeacherDora Admin
BECE 2019 - MATHEMATICS [PAPER II]
THEORY QUESTIONS
a
Given that X = {whole numbers from 4 to 13} and Y = {multiples of 3 between 2 and 20}, find X ∩ Y.
b
Find the Least Common Multiple (L.C.M) of the following numbers: 3,5 and 9.
c
If
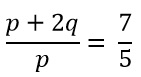
, find the value of
,
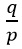
a
Solve:
.
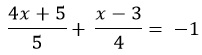
b
The ratio of boys to girls in a school is 12:25. If there are 120 boys.
i) how many girls are in the school?
ii) what is the total number of boys and girls in the school?
c
Simplify:
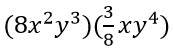
a
In an examination 60 candidates passed Integrated Science or Mathematics. If 15 passed both subjects and 9 more passed Mathematics than Integrated Science, find the:
i) number of candidates who passed in each subject;
ii) probability that a candidate passed exactly one subject.
b
Factorize: xy + 6x + 3y + 18
a
Express 250 % as a fraction in its lowest term.
b
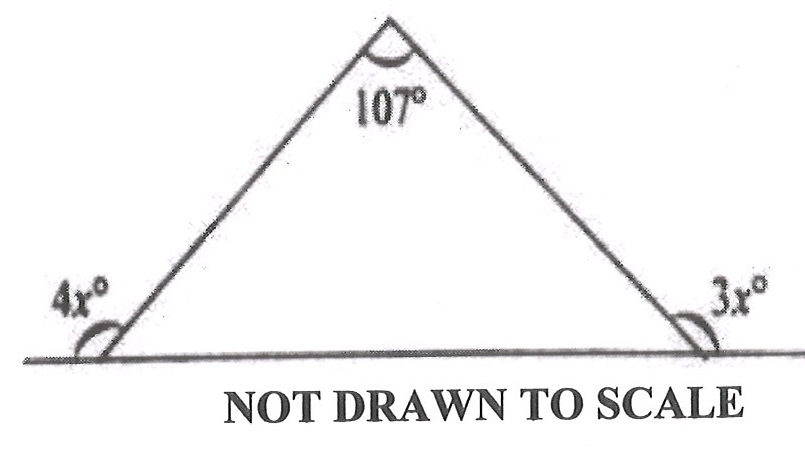
Use the diagram to find the value of x.
c
Simplify:
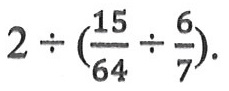
d
If q =
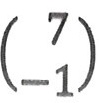
and r =
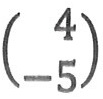
find (q + r).
a
x | 1 | 2 | 3 | 4 | 5 |
↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
y | 0 | 3 | 6 | 9 | 12 |
The mapping shows the relationship between x and y.
i)
using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the y-axis, draw two perpendicular axes 0x and 0y on a graph sheet for 1 ≤ x ≤ 5 and 0 ≤ x ≤ 14;
ii)
plot the point for each ordered pair, (x, y).
iii)
join the points with a straight line;
iv)
using the graph, find the gradient of the line in (a)(iii);
v)
use the graph to find the equation of the line in (a)(iii).
b
Simplify: 32 x 8 x 4 x 2, leaving the answer in the form 2n
The marks obtained by students in a class test were
4 | 8 | 7 | 6 | 7 |
2 | 1 | 7 | 4 | 7 |
3 | 7 | 6 | 4 | 3 |
7 | 5 | 2 | 7 | 2 |
5 | 4 | 8 | 3 | 2 |
a
Construct a frequency distribution table for the data.
b
Find the:
i)
mode of the distribution
ii)
median mark of the test;
iii)
mean mark.