TeacherDora Admin
BECE 2022 - MATHEMATICS [PAPER II]
THEORY QUESTIONS
(a)
Given that P = {factors of 36} and Q = {factors of 54},
(i)
list the members in the sets P and Q.
(ii)
Find:
Α
P∩Q
Β
n(P∩Q)
Γ
The Highest Common Factor (HCF) of 36 and 54.
(b)
Write down the next two terms of the sequence 1,4,9,...,...
(c)
The median of the ordered set of observations 2,3,(4m-3),(3m+1),11 and 13 in ascending order is 6. Find the value of m.
(a)
Simplify:
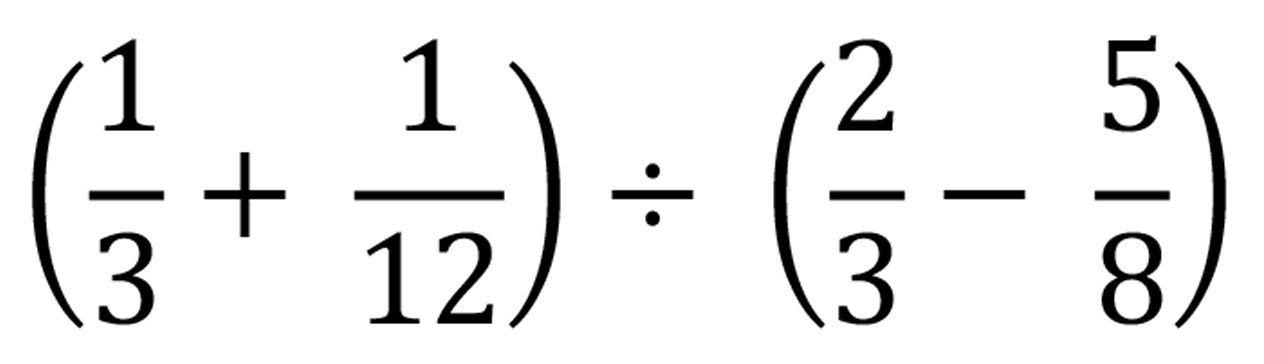
(b)
Find the product of (2x - 3) and (2x + 3).
(c)
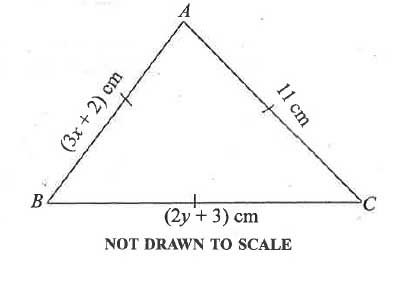
In the diagram, ABC is an equilateral triangle. Find the value of (x + y).
(a)
Given the relation
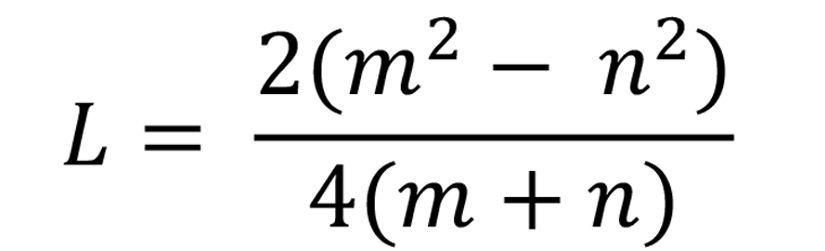
(i)
simplify L;
(ii)
find the value of L when m = 2 and n = 3.
(b)
Solve
.
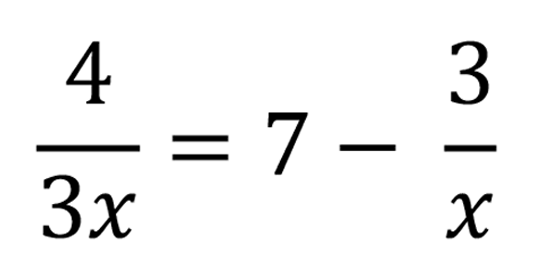
(c)
A salesman gets a commission of 51⁄2% of the value of items he sells. The salesman sells 12 textbooks at GH₵ 25.00 per book, 3 scientific calculators at GH₵ 50.00 per calculator and 8 packets of bic pens at GH₵ 50.00 per packet. Calculate the salesman's commission.
(a)
Fred is (x - 1) years old now. How old:
(i)
was he 4 years ago?
(ii)
will he be 8 years from now?
(iii)
is he now, if his age in 8 years time will be three times his age 4 years ago?
(b)
The perimeter of a rectangular cocoa from is 497 km. The length of the farm is 21⁄2 times the width. Find the:
(i)
width;
(ii)
length of the farm.
(a)
Factorize: (x-y)(3m+n)-(x-y)(m-2n)
(b)
Given that
,
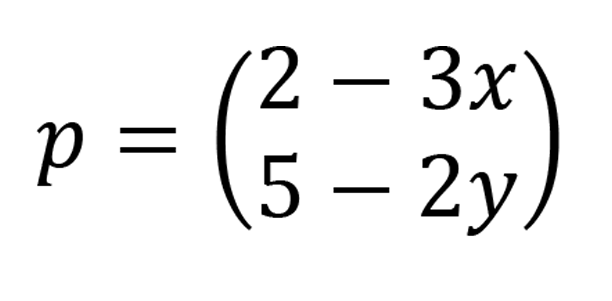
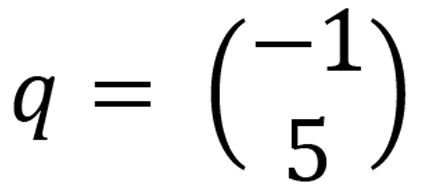
and
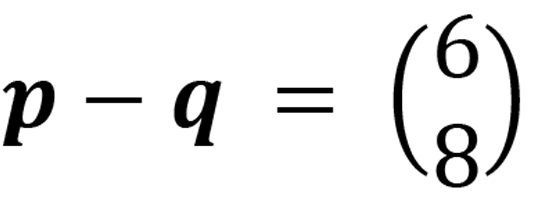
Find the value of (x + y)
(c)
(i)
Find the truth set of
.
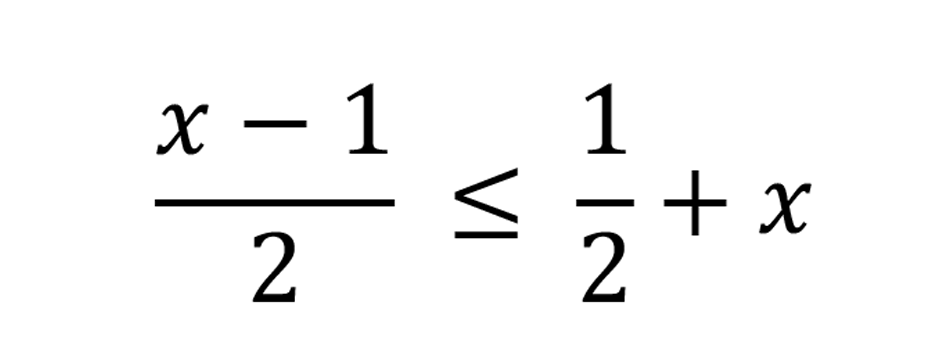
(ii)
Illustrate the answer in (i) on the number line.
(a)
Copy and complete the table for the relation y = 5 - 2x for -3 ≤ x ≤ 4.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 11 | 5 | 1 | -3 |
(b)
Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the y-axis, draw on a graph sheet two perpendicular axes ox and oy for -5 ≤ x ≤ 5 and -12 ≤ y ≤ 12.
(c)
(i)
Using the table, plot all the points of the relation y = 5 - 2x.
(ii)
Draw a straight line through all the points.
(d)
Using the graph, find the:
(i)
value of y when x = -2.6;
(ii)
value of x when y = -2.8;
(iii)
gradient of the line.