BECE 2024 - MATHEMATICS [PAPER II]
THEORY QUESTIONS
(a)
A fair die and a fair coin are thrown together once.
(i)
Write down the set of all possible outcomes.
(ii)
Find the probability of obtaining a prime number and a tail.
(b)
The map of a field is drawn to a scale of 1 : 100. If the width and area of the field on the map are 8 cm and 88 cm2 respectively, find in m2, the area of the actual field.
(c)
Copy and complete the 3 x 3 magic square such that the sum of the numbers in each row, column and diagonal is equal to 21.
| 10 | 3 | |
| 7 |
(a)
Given the vectors p =
(b)
A man shared an amount of money between his children Baaba and William in the ratio 6 : 5. Baaba received GH₵ 1,200.00
(i)
find the total amount shared.
(ii)
William invested his share in an account at the rate of 20% simple interest per annum for 2 years. Find the total amount in his account at the end of the 2 years.
(a)
Simply: 3
(b)
A wire of length 38 cm is bent into the shape of a rectangle whose length is 7 cm more than the width.
Find the area of the rectangle.
(c)
If 15% of the length of a rope is 720 metres, find half of the length of the rope.
(a)
Using a ruler and a pair of compasses only, construct ∆PQR such that angle PQR = 90°, |PQ| = 5.5 cm and |QR| = 8 cm.
(b)
Construct a perpendicular of PR from Q.
(c)
Locate M, the intersection of the perpendicular and PR.
(d)
Measure:
(i)
|MR|;
(ii)
|QM|.
(e)
Calculate, correct to the nearest whole number, the area of triangle QMR.
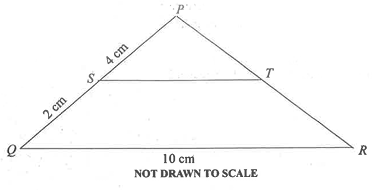
(a)
In the diagram, ∆PQR is an enlargement of ∆PST. |PS| = 4 cm, |QS| = 2 cm and |QR| = 10 cm.
(i)
Find the length of ST.
(ii)
If |PQ| = |PR|, find the area of ∆PQR
(b)
The total area of a school compound is 900
The areas of the Administration and Classroom block, Library and School Park are 300
Find the area covered by Roads and Walkways altogether.
(a)
Copy and complete the table for the relation F =
Where F and C are degrees Fahrenheit and degrees Celsius respectively.
| °C | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| °F | 32 | 68 |
(b)
Using a scale of 2 cm to 10 units on the vertical axis (°F) and 2 cm to 5 units on the horizontal axis (°C), draw a linear graph for the relation.
(c)
Use the graph to find the temperature in degrees celsius when F = 55 degrees.
(d)
Interpret the slope of the relation.


 TeacherDora Admin
TeacherDora Admin